Rätsel 1 - 20
- Nr 1 Der fehlende Franken
-
Drei Knaben kommen ins Spielwarengeschäft und kaufen sich einen Lederball. Der Verkäufer verlangt 24 Franken und jeder der Knaben zahlt 8 Franken. Kaum sind die drei aus dem Laden kommt der Chef des Ladens zum Verkäufer und macht ihn darauf aufmerksam, dass dieser Ball im Sonderangebot ist und nur 19 Franken kostet. Der Chef weist den Verkäufer an den drei Knaben nachzurennen und Ihnen den Fehlbetrag zurückzugeben. Der Verkäufer nimmt 5 Einfranken Stücke aus der Kasse und rennt nun den drei Knaben nach. Unterwegs denkt er sich, dass ja 5 Franken gar nicht durch drei teilbar ist und beschliesst jedem nur einen Franken zurückzugeben und den Rest von 2 Franken selber zu behalten.
Jeder der drei Knaben hat zuerst 8 Franken bezahlt und danach 1 Franken zurückbekommen macht also 7 Franken. Dreimal 7 Franken macht 21 plus 2 Franken die der Verkäufer behalten hat macht 23 Franken der Ball hat aber doch 24 Franken gekostet. Wo ist der fehlende Franken geblieben?
Nr 2 Schachbrett-Domino
Auf ein normales Schachbrett mit 64 Feldern, kann man 32 Dominosteine legen (jeder Dominostein belegt genau 2 Felder). Von diesem Schachbrett entfernt man nun zwei diagonal gegenüberliegende Eckfelder.
Ist es möglich die verbliebenen 62 Felder mit 31 Dominosteinen zu belegen? Wenn ja wie?
Nr 3 Die Amnestie des Königs
Anlässlich seines 50. Geburtstages will ein König einen Teil der 500 im Kerker sitzenden Gefangenen amnestieren . Dazu gibt der König dem Kerkermeister eine genaue Anweisung wie die Teilamnestie durchzuführen ist.
Beim 1. Durchgang dreht der Kerkermeister den Schlüssel im Schloss jeder Türe im Kerker. Beim 2. Durchgang den Schlüssel jeder 2. Türe. Beim 3. Durchgang den Schlüssel jeder 3. Türe. Beim 4. jeder 4. Türe und so weiter bis zur 500. Tür im Kerker.
Die Schlösser der Türen sind so gearbeitet dass Sie beim 1. Drehen offen sind beim 2. Drehen wieder geschlossen beim 3. wieder offen usw.
Wie viele der 500 Gefangenen können nach dieser Prozedur durch eine offene Türe in die Freiheit?
Nr 4 Die falschen Taler
In einer Kiste liegen 9 Säcke mit je 100 Talern. Ein echter Taler wiegt genau 20 Gramm. Einer der Säcke ist nun aber mit gefälschten Talern gefüllt die 5% leichter sind.
Wie ist es mit nur EINER Wägung möglich herauszufinden in welchem Sack die falschen Taler sind?
Nr 5 Das Türen Problem
Ein listiger Kaufmann wurde einst zu lebenslanger Haft veruteilt. Da er aber ein sonst unbescholtener Bürger war, wollte der Richter ihm noch eine Chance geben und stellte ihm folgendes Rätsel.
"Vor dir hat es 2 Türen, eine der Türen führt in den Kerker und die andere in die Freiheit. Vor jeder Tür steht je ein Wächter, einer der Wächter sagt immer die Wahrheit der andere lügt immer. Du weisst nicht welcher der Wächter die Wahrheit sagt aber du darfst einem EINE Frage stellen um herauszufinden welche der 2 Türen in die Freiheit führt."
Der Angeklagte stellte einem Wächter eine Frage, wusste dann genau welche Türe in die Freiheit führt und konnte sich so vor der Haftsrafe retten.
Was hatte er gefragt?
Nr 6 Der Frosch im Brunnen
Eines Tages fällt ein kleiner Frosch in einen 30 Meter tiefen Brunnen. Mit aller Kraft probiert der Frosch die glitschigen Wände des Brunnens hinauf zu klettern. Dabei klettert der Frosch pro Tag 3 Meter hinauf. Jede Nacht, während er sich ausruht, rutscht der Frosch aber wieder um 2 Meter nach unten.
Wie viele Tage dauert es bis der arme Frosch endlich aus dem Brunnen kommt?
Nr 7 Die drei Töchter
Zwei Mathematiker treffen sich auf der Strasse und fangen ein Gespräch an.
"Wie ich gehört habe hast du schon drei Kinder."
"Ja das ist richtig, ich habe drei Töchter."
"Wie alt sind sie denn?"
"Tja, wenn man ihr Alter zusammenzählt erhält man 13 und wenn man ihr Alter miteinander multipliziert ergibt das die selbe Zahl wie auf der Hausnummer dort drüben."
"Ach ja, das genügt mir aber noch nicht."
"Stimmt, ich muss noch erwähnen, dass meine älteste Tochter einen Hund hat."
"Jetzt ist alles klar!"Wie alt sind die drei Töchter?
Nr 8 Die 12 Marmorkugeln
Gegeben sind 12 Marmorkugeln. Bis auf eine Kugel sind alle gleich schwer. Diese eine jedoch ist entweder leichter oder schwerer als die anderen.
Wie ist es möglich, mittels einer Balkenwaage und DREI Wägungen herauszufinden welche der 12 Marmorkugeln ein anderes Gewicht hat?
Nr 9 Licht im Dunkeln
In einem fensterlosen Raum im Keller eines Hauses sind 3 einfache Glühbirnen angebracht 2 an der Wand und eine an der Decke. Neben der Eingangstüre befinden sich 3 Kippschalter, wobei jeder Schalter mit einer Glühbirne im inneren des Raumes verbunden ist.
Die Türe zum Raum ist geschlossen und so dicht dass kein Schimmer Licht aus dem Innneren nach aussen dringen könnte (auch nicht durchs Schlüsselloch!).
Man darf den Raum nur EINMAL betreten und nach dem Öffnen der Türe ist es nicht mehr erlaubt die Schalter zu berühren.
Wie ist es unter diesen Bedingungen möglich herauszufinden, welcher der 3 Schalter mit der Glühbirne, an der Decke des Kellerraumes, verbunden ist.
Nr 10 Von Forschern und Federn
Drei Forscher werden von Indianern gefangengenmommen und an drei hintereinander stehende Marterpfähle gebunden.
Dabei sieht der vorderste Forscher keinen der anderen Kollegen. Der zweite sieht einzig den Marterpfahl mit dem vordersten Forscher. Der dritte sieht vor sich die beiden Marterpfähle mit seinen beiden Kollegen.
Der Medizinmann steckt nun jedem der Forscher eine Feder ins Haar die er versteckt für den jeweiligen Forscher aus seinem Beutel herauszieht.
Nun spricht der Medizinmann zu ihnen: "Insgesammt hatte es zwei schwarze und drei weisse Federn in meinem Beutel. Ich gebe euch die Chance frei zu kommen, wenn einer begründet weiss, welche Farbe die Feder hat, die er angesteckt bekam. Aber wehe Ihr könnt die Antwort nicht begründen, dann werdet Ihr alle einen qualvolleren Tod als normalerweise finden!"
Sehr lange herrscht Stille, doch dann schreit einer: "Hurra, jetzt weiss ich es!"
Welcher Forscher war es und welche Farbe hatte seine Feder?
Nr 11 Überlappende Quadrate
Zeichne folgende blaue Figur mit einem zusammenhängenden Strich ohne dabei eine Linie mehr als einmal zu benutzen!

Nr 12 Der Klotz
Eines Tages bekam ein Schreinergeselle von seinem Meister eine Aufgabe. Er sollte eine Holzarbeit wie unten abgebildet herstellen, bei der der untere wie auch der obere Teil aus je EINEM Stück besteht. (die Rückseite des Holzblocks sieht übrigens genau gleich aus wie die abgebildete Vorderseite)

Der Geselle meinte daraufhin: "Meister ich mag ja ein guter Schreinergeselle sein aber zaubern kann ich nicht, dieser Klotz lässt sich unmöglich aus nur zwei Stücken fertigen!"
Ob der Geselle wohl recht hat?
Nr 13 Schlagende Uhren
Ein Uhrmacher hat in seinem Wohnzimmer zwei wunderschöne Uhren mit Schlagwerk, die jeweils zur vollen Stunde die Uhrzeit schlagen. Obwohl sie schon einige Jahre alt sind, gehen beide dank guter Pflege auf die Sekunde genau. Der einzige Unterschied zwischen den beiden Uhren ist folgender. Uhr 1 schlägt doppelt so schnell wie Uhr 2.
Wärend der Uhrmacher in seinem Sessel im Wohnzimmer sass und Zeitung las ist er eingeschlafen. Als er aufwachte hörte er noch einen Schlag bei dem beide Uhren gemeinsam schlugen und dann schlug Uhr zwei noch 2 mal alleine.
Wieviel Uhr war nun?
Nr 14 Der Geburtstag
Hans hat heute Geburtstag, wird 33 und ist damit 3 Mal so alt, wie Franz war, als Hans so alt war, wie Franz heute ist.
Alles klar? Nun wie alt ist Franz heute?
Nr 15 Eine verflixte Reihe – I
Welches wären die drei nächsten Buchstaben der folgenden Reihe:
E Z D V F S S A N Z
Nr 16 Die Gnonoz
Auf einem fernen Planeten lebt ein Volk dass sich Gnonoz nennt. Dieses Volk ist in drei Stämme unterteilt die Xurs die Schrogs und die Yzys. Ein Xur sagt immer die Wahrheit ein Schrog lügt immer und ein Yzy lügt oder sagt die Wahrheit je nach Lust und Laune.
Ein Händler der über dieses Volk bescheid wusste landete eines Tages mit seinem Raumschiff auf dem Planeten und traf kurz nach der Landung drei Gnonoz. Er begrüsste die drei und fragte sie von welchen Stämmen sie kommen.
Der 1. Gnonoz sagt: "Der dritte ist ein Schrog."
Der 2. Gnonoz sagt: "Der erste ist ein Xur."
Der 3. Gnonoz meint: "Ich bin ein Yzy."
Wer ist nun was, wenn von jedem Stamm ein Gnonoz dabei ist?
Nr 17 Der Spion
Ein französischer Spion wollte in eine englische Stadt eindringen. Dazu musste er aber den Wachen am Stadttor die richtige Parole nennen die er leider noch nicht wusste. Er legte sich also nahe des Stadttores versteckt in einem Busch auf die Lauer und wartete.
Kurz darauf kommt ein Händler auf einem Karren und verlangt Einlass. Der Wächter sagt: "28, was ist deine Antwort?". Der Händler antwortet mit 14 und wird eingelassen.
Dann kommt eine junges Bauernmädchen und nun sagt der Wächter: "8, was ist deine Antwort?". Das Mädchen antwortet mit 4 und wird eingelassen.
Später steht ein Mönch vor den Stadttoren und der Wächter sagt: "16, was ist deine Antwort?". Der Mönch antwortet mit 8 und wird eingelassen.
Der Spion glaubt nun alles zu wissen und stolziert mit einem breiten Lächeln vor die Stadttore. Der Wächter verstellt ihm den Weg und sagt: "12, was ist deine Antwort?". "Ich sage 6!" antworted der Spion und will weiterlaufen aber bevor er auch nur einen Schritt machen kann, zieht der Wächter sein Schwert und tötet den Spion.
Tja der Spion hatte die falsche Zahl genannt! Aber was wäre denn richtig gewesen?
Nr 18 Der Alchimist
Ein Alchimist stellte seinem Schüler eine Aufgabe. Er zeichnete mit blauer Kreide einige Zeichen an die Wand.
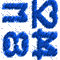
Nun verlangte er von seinem Schüler: "Zeichne mir die nächsten 2 Zeichen!"
Wie die wohl aussehen?
Nr 19 Die Lastwagenkolonne
Ein Kolonne von 10 Lastwagen muss über eine schmale Holzbrücke fahren, deren Länge ein gerades vielfaches der Länge eines Lastwagens ist. Die Brücke darf maximal mit dem Gewicht von 8 Lastwagen belastet werden Um dies zu erreichen fahren die Fahrer mit einem Abstand von genau einer halben Wagenlänge hintereinander mit konstanter Geschwindigkeit über die Brücke. Vom Moment an wo der erste Wagen auf die Brücke fährt bis zum Zeitpunkt wo der letzte die Brücke verlässt vergehen 10 Minuten und 12 Sekunden.
Wie lange dauert die Überfahrt eines Lastwagen?
Nr 20 Eine verflixte Reihe – II
Wie sehen die nächsten zwei Reihen aus?
11 12 11 2 1 11 1 1 2 2 13 1 2 2 1 1










